Get Inspiration, Delivered.
Join our newsletter and get inspiring projects, educational resources, and other cool metal stuff, straight to your inbox.
The Zahner R&D team recently wrapped a productively spent summer. Intern Elena Vazquez, a Master of Architecture candidate and Fulbright Scholar from Penn State University, joined the team for 10 weeks to conduct research on how to efficiently manufacture double curved metal surfaces. With the uptick in demand for gracefully curving architectural forms, R&D lead engineer and researcher, James Coleman, challenged Vazquez to discover a novel and cost-effective way of fabricating the designs our clients develop.

Renderings courtesy ICD/ITKE, Bjarke Ingels, ZHA, Hernan Diaz Alonso.
The challenge
Creating single curvature into sheet metal is easy — like rolling a piece of paper into a tube — but double curvature presents significant challenges in manufacturing. Aside from being difficult to produce, stretching a flat surface in two directions challenges the constraints of the material itself. If overworked, metal surfaces become brittle, lose strength and are prone to poor surface quality – certainly not desirable in architectural (or any other) applications.
Current Solutions for Double Curved Metal Surfaces
Current solutions for double curving metal include spinning, stamping, hammering, explosion forming, cold working, die casting and multi-point stretch forming.
Cold working forces metal panels into a pre-built frame. While this methodology has been used to approximate double curvature, the resulting aesthetic can appear ‘choppy’ and less than precise.
Die casting/stamping involves fabrication of a mold for each unique shape followed by either pouring hot metal or stamping into it; both require post processing of the surface once complete. The necessary steps are highly time consuming and prohibitively expensive for bespoke architectural application.
Multi-point stretch forming techniques achieve graceful double curve forms with a multipurpose mold, but similar to die casting, developed machinery remains very expensive to buy and maintain. Coleman and Vazquez questioned:
What if there were a less expensive and more efficient way to accomplish the same graceful and precise double curves?
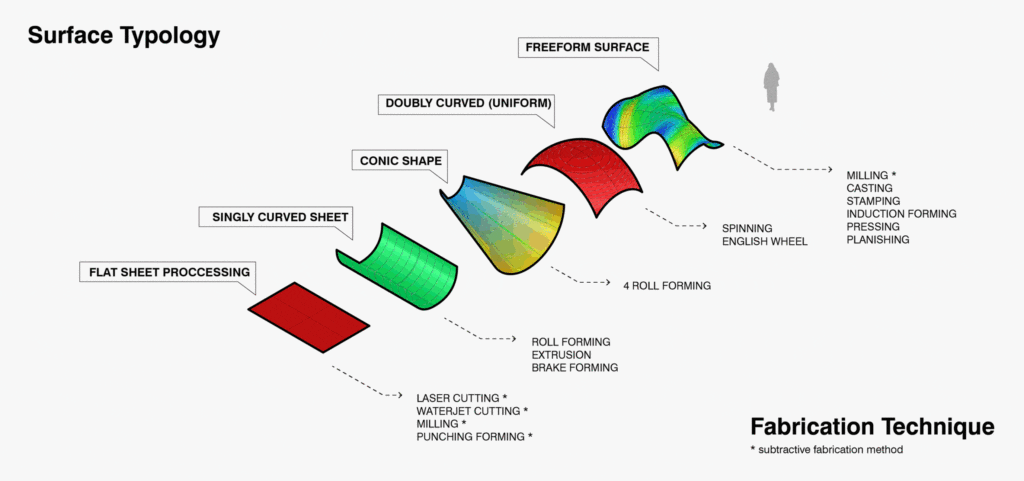
Image © A. Zahner Company.

PHOTO © A. ZAHNER COMPANY

Photograph by Virgile Simon Bertrand, courtesy ZHA.
THE ENGLISH WHEEL – AN OLD APPROACH TO CREATING DOUBLE CURVES
The English Wheel, or wheeling machine, allows artisans to create double curves by hand working metal sheets between two radiused wheels. The tool is best known for its use in creating bespoke car parts – think of the elegant fenders of the 1930s and 1940s.
Mastering use of the English Wheel is an art form, requiring a keen sense of touch and depth of material expertise. Artisans spend years honing skills required to perfect wheeling techniques. The curves achieved are precise and graceful, but producing bespoke panels in this way is labor intensive and expensive. A single building might contain several thousand uniquely shaped panels, making conventional wheeling impossible. Yet, the machine itself is simply constructed and economical. The team wondered:
Might we offset the costs of doubly curved surfaces with a fresh take on the English wheel, combining the precise motion and force control of robotics with this tried and true method for shaping metal?
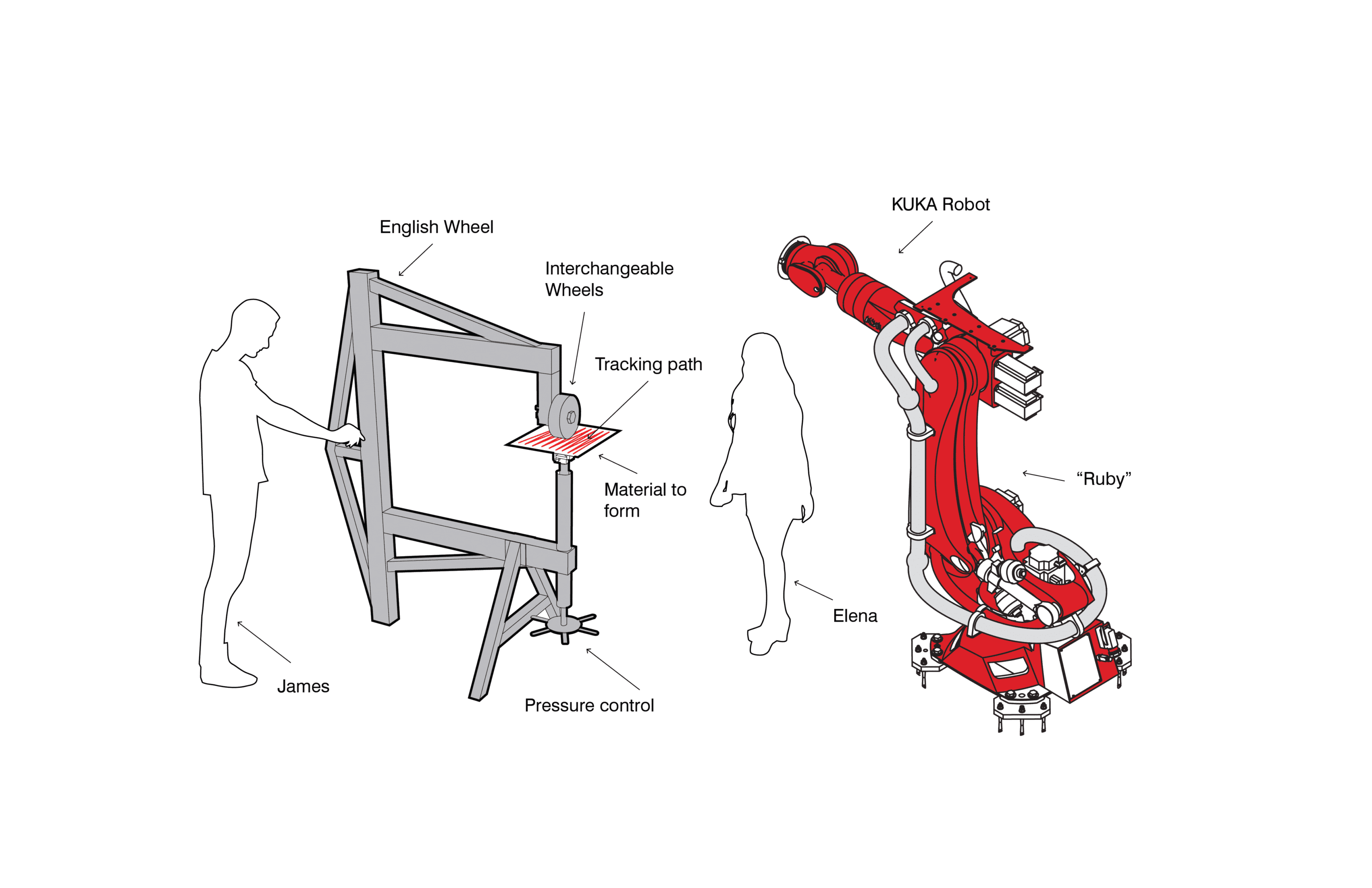
THE SOLUTION – A NEW APPROACH TO CREATING DOUBLE CURVED METAL SURFACES
A year ago, Zahner introduced Ruby, a Kuka KR270 R2700 robot, with the intention of testing novel ways of incorporating robotics into manufacturing processes. Ruby has since become an integral part of the R&D team, proving herself invaluable in testing theoretical and practical applications. For the double curvature challenge, the theory was if Ruby could be ‘taught’ to form panels, we would be poised to dramatically expand what is possible to build in architecture.

PHOTO © A. ZAHNER COMPANY.
HYPOTHESIS and TESTING
Prior to programming the robot, predictive wheeling paths needed to first be generated through digital surface analysis to establish desired curves. Using a theoretical, undulating shape, Vazquez demonstrated various surface typologies, identifying areas where double curved panels would be required. Recursive subdivision of the surfaces based on Gaussian curvature values generated “points of interest” and stretch values automatically. Each of these points contained principal directionality and were strung together into wheeling paths predicted to generate the desired shapes. At its core, the point to point path hypothesis is a computationally sophisticated game of connect the dots.
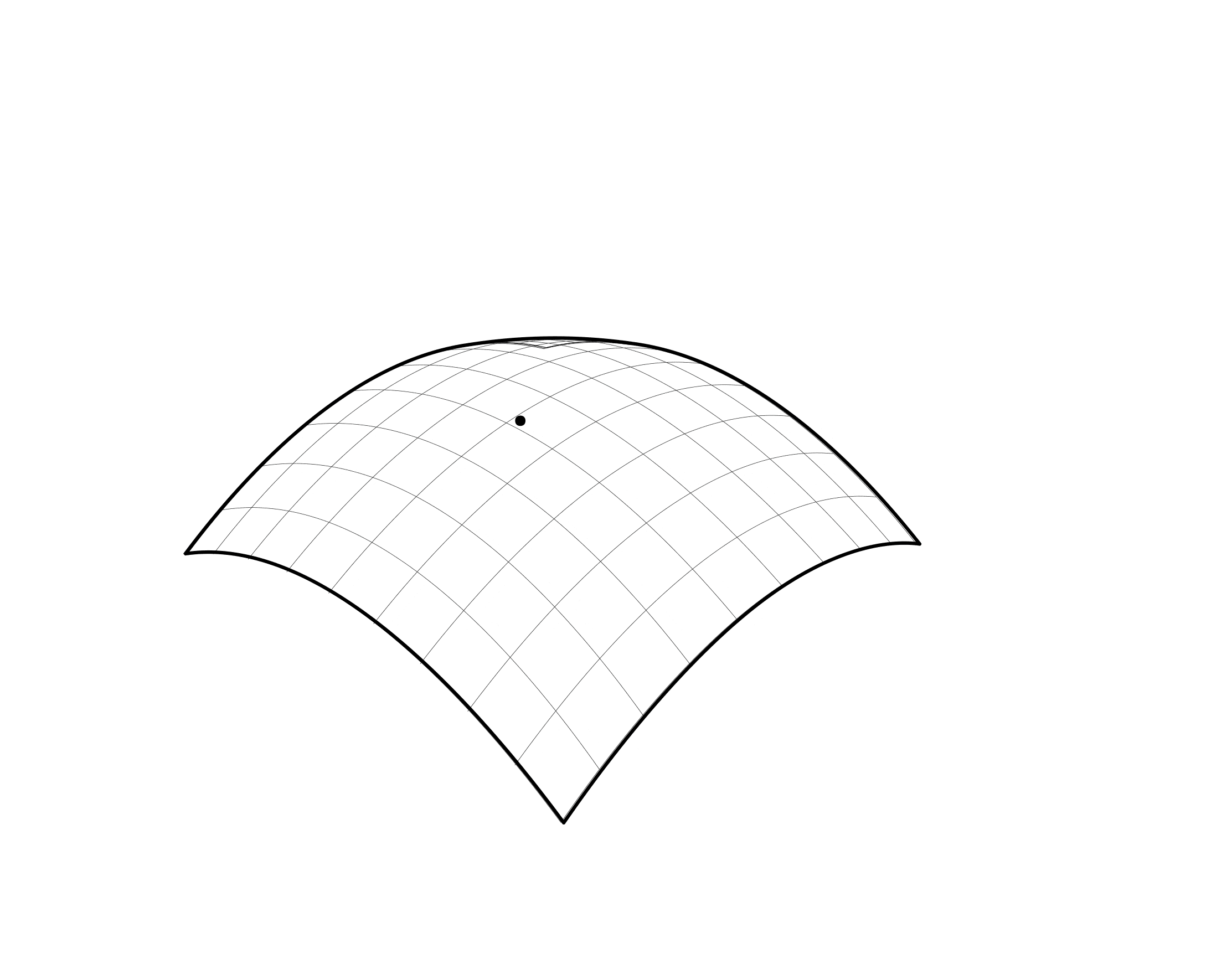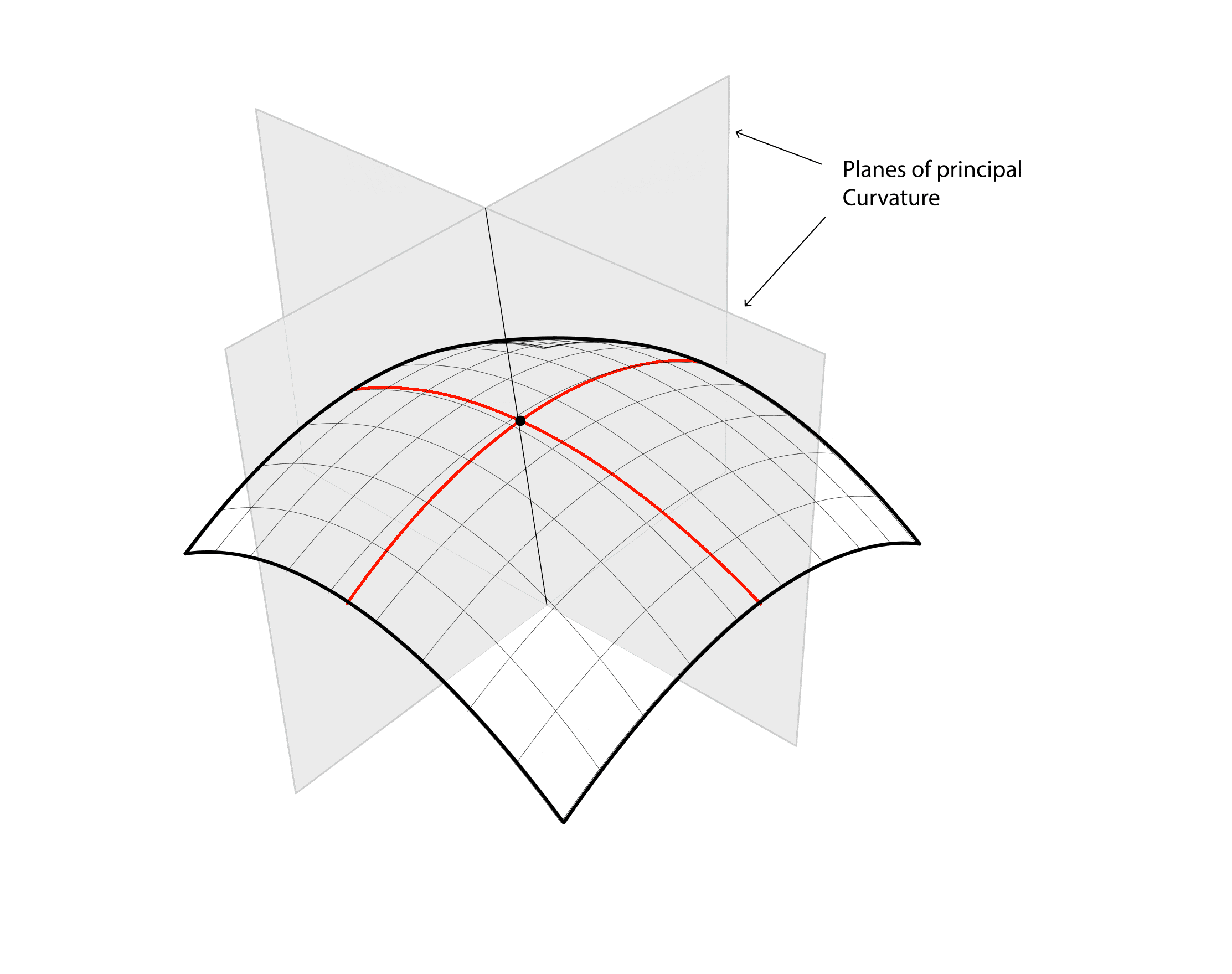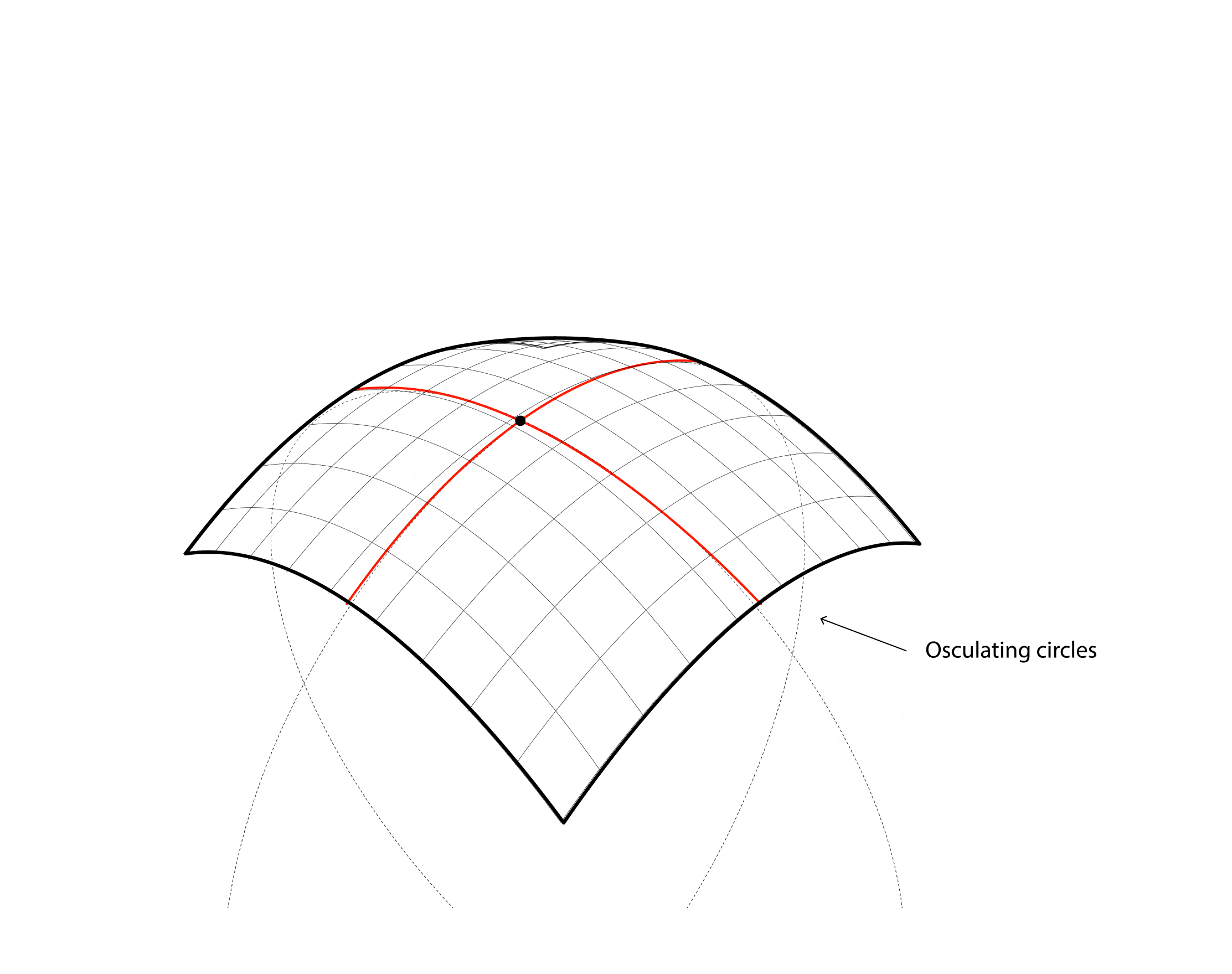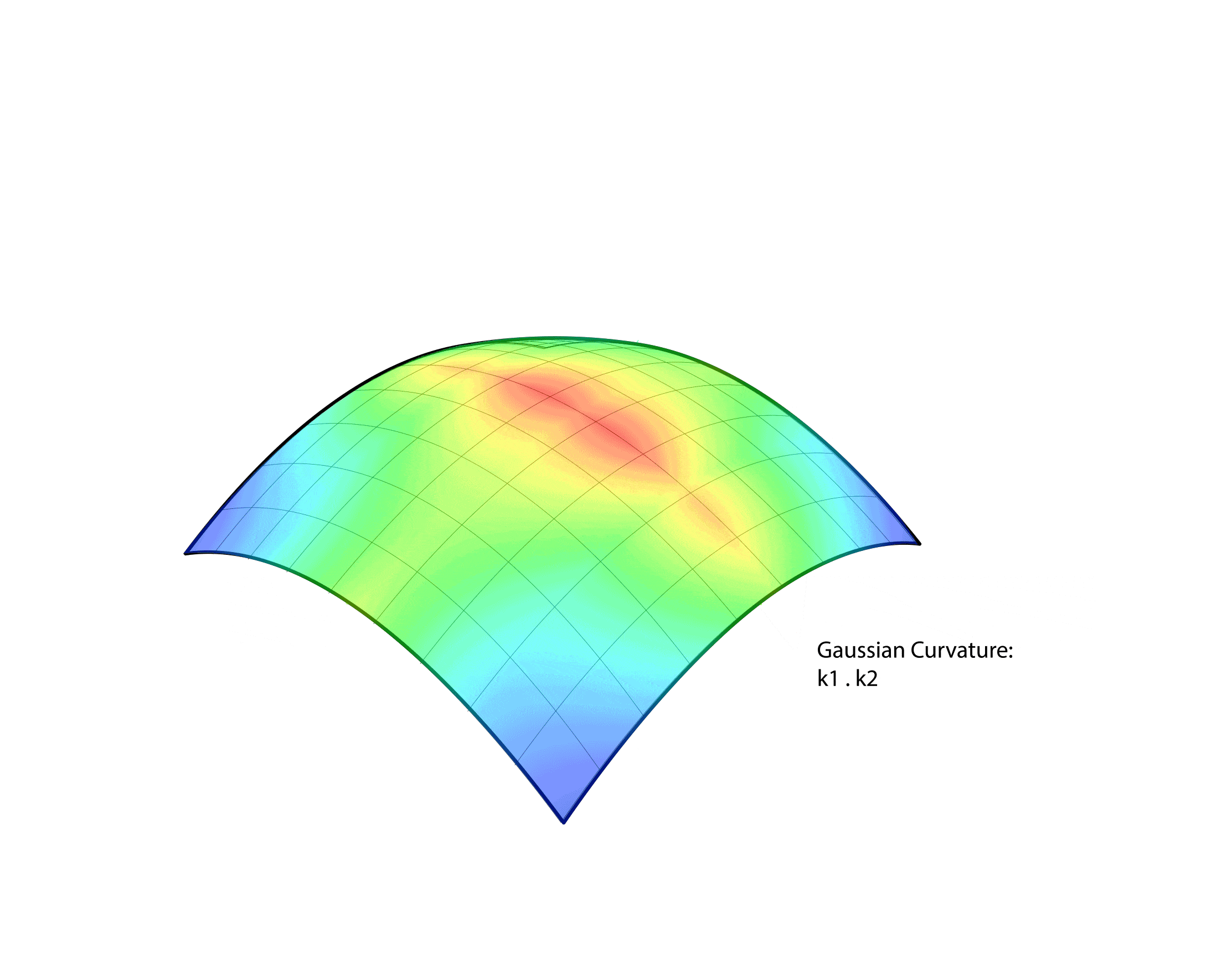


The magic is in the interpretation of Gaussian values and prediction of material behavior. Numerous digital simulations and analyses were undertaken within Grasshopper and Kangaroo to create the wheeling paths.
These preliminary paths were tested by manually wheeling to prove the point to point path theory. Testing was key in fine tuning the point/path workflow and in establishing the precise pressure and wheel size required to form each unique panel geometry.
Following human testing, it was time to see if Ruby could form the material herself. First, she had to ‘learn’ the precise contact point locations, which were programmed using Grasshopper and KukaPrc software. After several test runs, the team discovered that Ruby needed to ‘learn’ how to pivot the material in the same fluid way that a human hand would to avoid material drag. Once resolved, the creation of individual panels and curvature testing began to inform refinement of established path theories.

PHOTO © A. ZAHNER COMPANY.
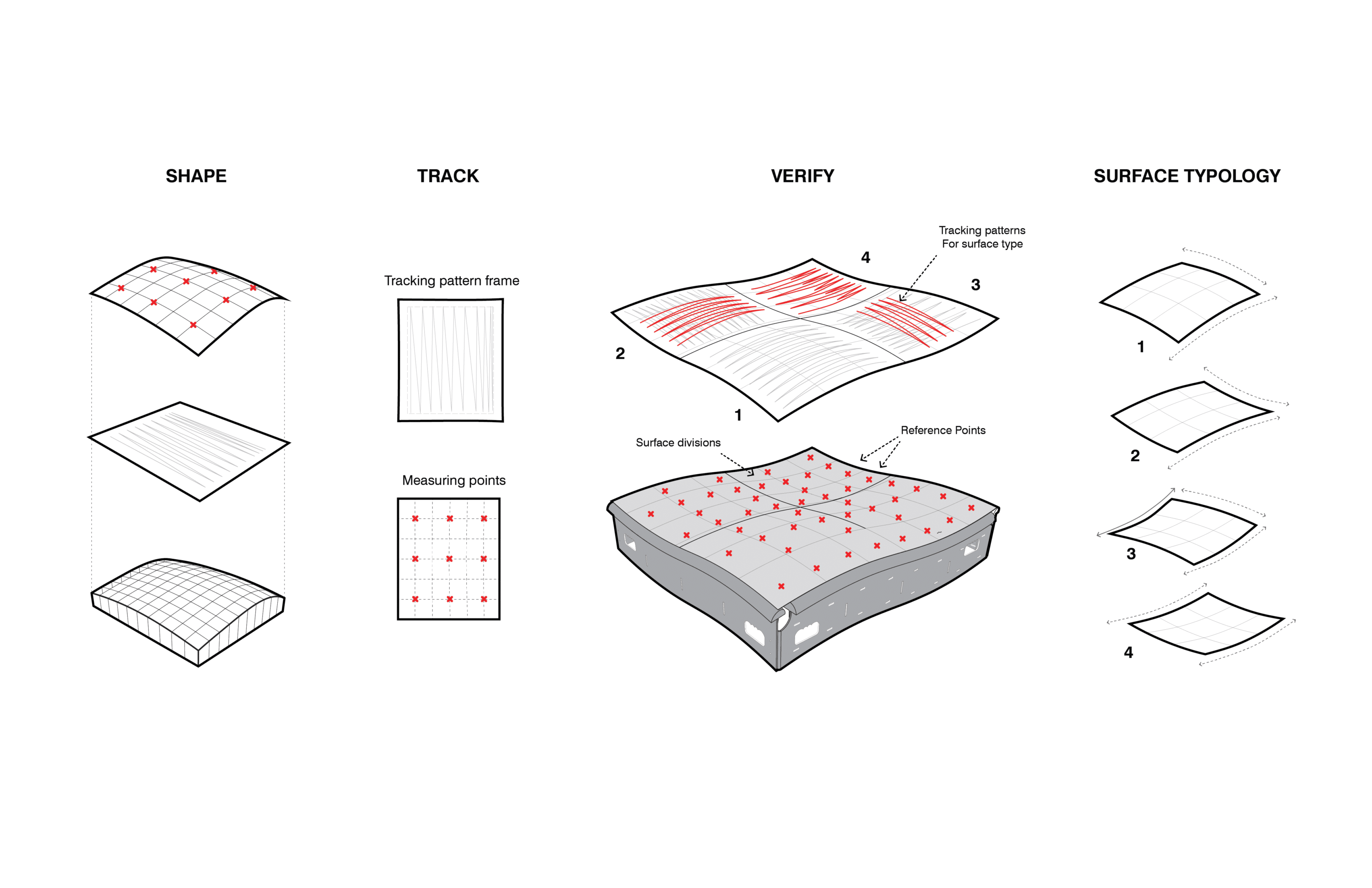
JIG CREATION + MEASUREMENT
Measuring curvature is a highly involved process. Construction of a 4 x 4 ft. structural aluminum jig allowed the team to overcome measuring challenges, resulting in a method to quickly and easily decipher testing results. Measuring holes were drilled into the side of the structure at regular intervals, and a measuring tool, created in Rhino and 3D printed onsite, allowed for rapid synthesis of curve information. If a panel’s reference point did not connect with the measuring tool once inserted in the measuring hole, it required further refinement.

PHOTO © A. ZAHNER COMPANY.
CONCLUSION
During Vazquez’s 10 short weeks, the R&D team made incredible progress toward resolving the issues surrounding double curvature fabrication. While substantiating the point to point path hypothesis will require further testing, the possibility for future fabrication using Ruby and the English Wheel is promising.

PHOTO © A. ZAHNER COMPANY.






